EL ABC DE LAS ANTENAS
2. La resonancia de un dipolo
Por Luis A. del Molino EA3OG (ea3og@ure.es)
La resonancia de un dipolo de media onda
En el capítulo inicial, explicamos que, si hacemos llegar una tensión alterna de alta frecuencia (RF) al centro de dos trozos de cable alineados, cada uno de los cuales tiene una longitud de ¼ de longitud de onda correspondiente a la frecuencia de esa RF suministrada (Figura 1 y 2), conseguiremos que la onda de repulsión electrónica cuando alcanza los puntas de cada extremo del cable y vuelva rebotada , llegue en fase con el cambio de signo de la tensión que le llega en el siguiente semiciclo por el cable en el punto de alimentación. De este modo, se pasee de un extremo a otro de la antena, cambiando de signo a un ritmo igual al de la frecuencia de la tensión alterna de excitación (RF).
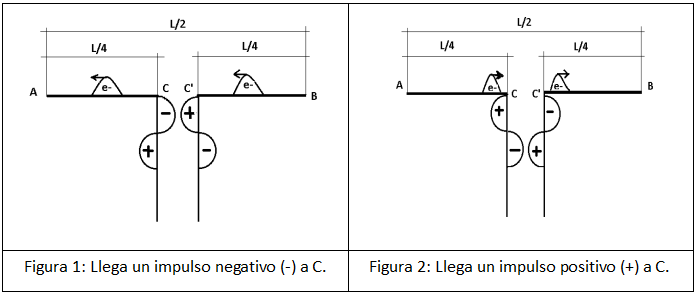
En efecto, si el impulso eléctrico negativo (-) recorre L/4 hasta la punta A y luego rebota hacia el centro C, habrá hecho un recorrido de L/4 (CA) + L/4 (AC) = un total de L/2. Cuando vuelve rebotado al centro C, allí ahora ha transcurrido medio ciclo y hay un impulso de signo contrario (+) (Figura 2), que está encantado de recibir electrones y absorberlos, pues es a lo que se dedica ahora. Al mismo tiempo, el impulso de repulsión negativo ahora lo envía por C’ hacia el extremo B y allí se produce el mismo rebote, pero ahora en el extremo opuesto B. Y así sucesivamente en los siguientes hemiciclos (mitad de un ciclo completo).
El impulso de repulsión se pasea de punta a punta por la antena ACC’B (como si fuera un solo cable continuo de media onda). El impulso rebota en las puntas y se ve reforzado en el centro por los impulsos sincrónicos que le siguen llegando por los cables de alimentación y se refuerzan mutuamente, con lo que aumenta enormemente la amplitud del movimiento de los electrones y se alcanza un estado que llamamos resonancia. En este estado la tensión (presión) en las puntas A y B es máxima y opuesta, tanto positiva como negativa , y la corriente de electrones es máxima en el centro C-C’ y mínima en las puntas A y B (prácticamente nula, salvo las fugas de electrones al aire en las puntas).
En el siguiente semiciclo (el otro medio ciclo) (Figura 2), las tensiones se invierten en las puntas A y B y la corriente electrónica en el centro C-C’ cambia de signo y se dirige hacia el lado contrario.
¿Por qué hablas de que la corriente circula entre C y C’ si el dipolo está interrumpido allí?
Porque los mismos electrones (la misma cantidad) que salen por C , entran por C’ y se dirigen hacia B, por lo que en la práctica es como si el cable no estuviera cortado, puesto que no se distingue ni nota el corte, pues todo funciona como si C y C’ estuvieran conectados entre sí.
Lo que sale por C entra por C’ y viceversa. Las dos corrientes son iguales y opuestas, no se pueden distinguir y nosotros no le diremos al cable que está partido, por lo que se crea exactamente el mismo campo magnético en el entorno, gracias a la existencia de una corriente que circula hotizontal en C y C’ que rebota por toda la antena de punta a punta, como si ambos puntos estuvieran unidos.
Tensiones y corrientes en un dipolo de media onda resonante
Si tenemos un dipolo resonante bien cortado a la medida y alimentado con una tensión alterna de RF a la frecuencia de resonancia, en el dipolo de media onda, a la frecuencia de resonancia, todo el dipolo oscila con tensiones y corrientes en fase. Eso significa que pulsan al mismo tiempo y que, en cualquier punto por el que cortemos el dipolo (distinto del centro C-C’), hay una tensión y una corriente que se corresponden con las que habría en una resistencia pura (de valor según el punto donde cortemos), sin corrientes fuera de fase en relación a la tensión (Figura 3).
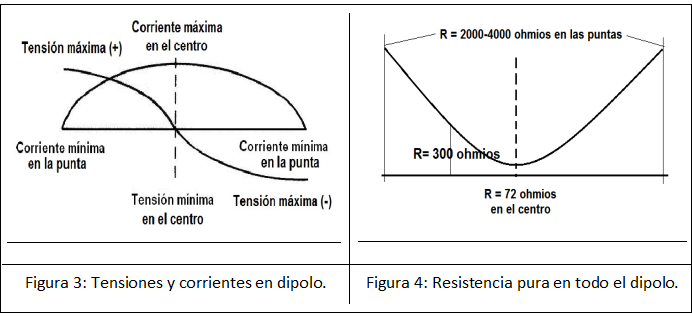
En las puntas del dipolo la tensión y la corriente corresponden a una resistencia muy elevada, porque la tensión es máxima y la corriente mínima. De modo que aplicando la Ley de Ohm (R = V/I), al ser la corriente I prácticamente nula, el denominador en el que se encuentra I tiende a cero, por lo que la R tiende a infinito (Figura 4), aunque como máximo alcanza unos 4000 ohmios en tiempo seco y 2000 ohmios en tiempo muy húmedo, debido a la mayor conductividad del aire húmedo, por culpa de las fugas de electrones en ambas puntas A y B.
En el centro del dipolo se da un punto en el que la corriente y la tensión de RF corresponde a la resistencia más pequeña, cuyo valor si el dipolo estuviera en el espacio libre sería de 72 ohmios, muy adecuado para conectar allí cables coaxiales de 75 y 50 ohmios. Sin embargo, debido a que en la vida real un dipolo se encuentra a una determinada altura sobre el suelo, normalmente a alguna fracción de su longitud de onda, esta impedancia resistiva oscila entre 50 y 100 ohmios, dependiendo de la altura.
Eso se debe a que la onda electromagnética reflejada en el suelo, cuando vuelve rebotada hacia la antena, afecta a las corrientes del propio dipolo y refuerza o disminuye su oscilación. La refuerza cuando la antena se encuentra a alturas múltiplos de ½ de onda y la corriente aumenta, por lo que la resistencia disminuye hacia 50 ohmios. A alturas múltiplos impares de ¼, la reflexión en el suelo tiende a frenar la corriente en la antena y, por tanto, la resistencia aumenta y se acerca más bien a 100 ohmios.
En algún punto fuera del centro (por ejemplo en la antena Windom), la resistencia que encontramos depende del punto de conexión y puede encontrarse con un valor intermedio (entre 50 y 2000 ohmios), por ejemplo 200, 300 o 600 ohmios, muy adecuada para bajadas de cables paralelos, puesto que disponemos de cintas de cables paralelos con dieléctrico de polietileno e impedancias de 300 (polietileno sólido) y 450 ohmios (polietileno con ventanitas).
Tensiones y corrientes en un dipolo NO resonante: impedancia
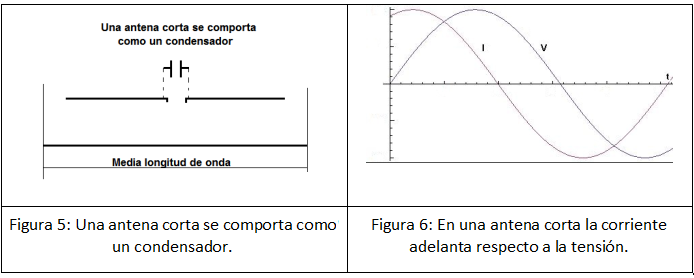
Si la antena es más corta de ½ onda (Figura 5), en el centro del dipolo aparecen reflejados electrones (impulso de corriente) que llegan antes de lo previsto. La corriente se adelanta a la tensión (Figura 6) y la antena se comporta como un condensador y aparece como una cierta reactancia capacitiva que disminuye la corriente en el dipolo. Sumada a la resistencia pura de la resonancia, da lugar a lo que llamamos reactancia capacitiva.
La impedancia Z es el resultado de la suma vectorial de dos factores: la resistencia y la reactancia capacitiva. Se representa por las letras Z = Rr - jXC,, en la que aparece un nuevo término “jXC“ que indica la aprición de la reactancia capacitiva que no se puede sumar directamente, sino vectorialmente y con signo negativo para indicar que es capacitiva.
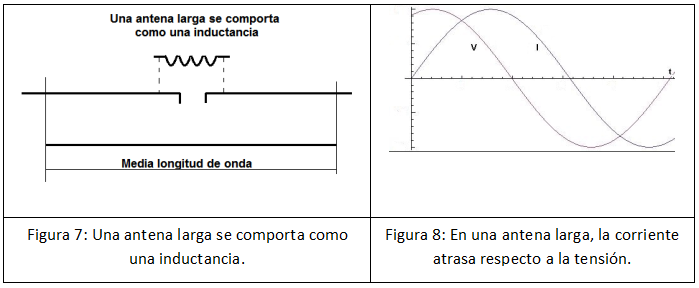
Si la antena es más larga de ½ onda (Figura 7), en el centro del dipolo aparecen reflejados electrones (en realidad la repulsión que impulsa a los electrones = corriente) que llegan más tarde de lo previsto y se adelantan al cambio de tensión en el punto de alimentación. La corriente va atrasada respecto a la tensión inductora (Figura 8) y la antena se comporta como una inductancia, por lo que aparece una cierta reactancia inductiva que disminuye la corriente de resonancia en el dipolo. Como consecuencia es como si a la resistencia se añadiera una inductancia en serie que da lugar a una resultante llamada impedancia inductiva. La impedancia es la suma de ambos factores: la resistencia y la reactancia inductiva y se representa mediante Z = Rr + jXL, donde “jXL” representa la reactancia inductiiva que no se puede sumar directamente sino vectorialmente.
El resultado de las corrientes desfasadas en el dipolo es un desajuste que da lugar a que una cierta potencia no la absorba la antena y vuelva reflejada desde la antena hacia el transmisor, con lo que en el cable que lleva la energía hasta la antena, se produce el fenómeno de la existencia de una onda directa y una reflejada, que se suman y restan dando lugar a lo que llamamos Ondas Estacionarias. Pero este fenómeno lo veremos con todo detalle más adelante en otros capítulos.
El concepto de resistencia de radiación
La resistencia que aparece en el centro de un dipolo resonante es prácticamente igual a la resistencia de radiación y es la menor resistencia que aparece en cualquier punto del dipolo (normalmente en el centro) y se llama así porque, gracias a ella, la antena se comporta enviando al espacio toda la energía recibida en forma de onda electromagnética, exactamente igual que una resistencia cuando convierte toda la energía que recibe y la convierte en calor.
Para cuantificar la resistencia de radiación, es decir medir la capacidad de convertir toda esa energía en onda electromagnética, utilizamos el valor de la resistencia equivalente que la convertiría en calor. Por tanto, en la práctica, en un dipolo de media onda resonante, la resistencia que aparece en el centro es casi toda ella resistencia de radiación Rr., aunque algo se pierde en la resistencia ohmica del cable en la llamada resistencia de pérdidas Rp que generalmente es despreciable por lo pequeña.
Nota: En el espacio totalmente libre, la resistencia que aparece en el centro C-C’ de un dipolo es de 72 ohmios, pero en el mundo real, con la antena situada sobre una tierra poco o muy conductora, esta resistencia oscila entre 50 y 100 ohmios. También si inclinamos las ramas hacia el suelo y le damos forma de V invertida, la resistencia de radiación baja hacia los 50 ohmios, un valor perfecto para conectar un cable coaxial de esta impedancia.
¿La resistencia de radiación es constante?
No, en absoluto, porque depende del punto en el que alimentemos la antena. Si la alimentamos en el punto de mínima resistencia (el centro), será muy baja (100-75-50 ohmios), pero si la alimentamos en cualquier otro punto será más elevada, pudiendo alcanzar valores de 200-300-600 ohmios en las antenas Windom y hasta 2000-4000 en las puntas en las antenas EndFed alimentadas en un extremo.
La resistencia de pérdidas
Solo una pequeñísima parte de esa energía que envía el transmisor se pierde en el cable de la antena en forma de calor, debido a su propia resistencia de conducción y esa resistencia es la resistencia de pérdidas Rp que aparece en serie con la Rr.
De modo que la resistencia que encontramos realmente en el centro de las antenas resonantes al final de nuestro cable de alimentación es realmente la suma de dos resistencias: la resistencia de radiación Rr y la resistencia de pérdidas Rp.
Fórmula de la Resistencia en el punto de alimentación: R = Rr + Rp.
La resistencia Rp en antenas resonantes de medidas normales (media y cuarto de longitud de onda) es inferior generalmente a 1 ohmio (algunas décimas de ohmio) y podemos olvidarnos de ella tranquilamente, porque es despreciable frente a la resistencia de radiación normalmente cercana a 50 ohmios.
El efecto Skin o pelicular
Desgraciadamente, la resistencia de pérdidas real a frecuencias de radio es muy superior a la resistencia óhmica de un conductor, esa que podemos medir con un óhmetro, y todo por culpa de un efecto que llamamos pelicular (en inglés efecto Skin).
Se trata de que en el centro de un conductor (Figura 9) se produce una acumulación de campos magnéticos A+B+C+D de todos los filetes conductores periféricos, igual que en el centro de un solenoide, y que dan lugar a una mayor autoinducción magnética en el centro del conductor muy superior a la de los filetes de la periferia o de la superficie del conductor. Esta autoinducción ocasiona una reactancia inductiva considerable en el centro del conductor, que disminuye del centro a la periferia, lo que hace que dificulte el paso de la corriente por el centro del conductor y, en la práctica, es como si disminuyera la sección útil conductora de un cable de cobre.
En consecuencia, la corriente de RF circula realmente por la parte más exterior del hilo de cobre, de forma que la resistencia real a la radiofrecuencia es muchas veces superior a la óhmica del conductor y, además, esa resistencia aumenta con la frecuencia de la corriente alterna de RF.
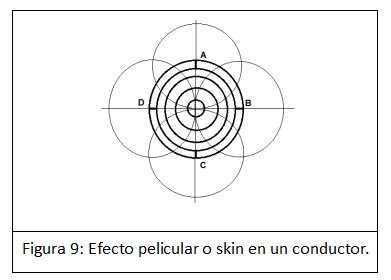
¿Cuánto superior? Depende del diámetro del hilo. Podemos estimar que puede llegar a ser fácilmente entre 10 a 100 veces la resistencia que podemos medir con un óhmetro de corriente continua.
A pesar de todo esto, el valor de una resistencia de pérdidas Rr de un cable de antena entre 1 y 3 mm (que son los que acostumbramos a utilizar en nuestras antenas) la resistencia de pérdidas real, incluido el efecto pelicular, es prácticamente despreciable e inferior a un ohmio, por lo que podemos estar seguros de que la resistencia de pérdidas Rp << Rr (la resistencia de radiación) de nuestra antena de media onda es generalmente despreciable y podemos considerar casi siempre en la práctica que la resistencia en el punto de alimentación R de una antena resonante es igual a la resistencia de radiación Rr.
Antenas muy pequeñas
El problema de las antenas muy pequeñas en relación a la media longitud de onda es que disminuye mucho su resistencia de radiación Rr y, si empieza a ser de un orden comparable a la resistencia de pérdidas Rp, y ya no podremos despreciarla, sino que deberemos tenerla muy en cuenta , así que deberemos estudiar muy bien cómo disminuir esta resistencia de pérdidas en todo lo posible, cuando normalmente no nos preocupamos de ella.
En efecto, ponngamos por ejemplo que tenemos una antena dipolo de media onda en V invertida con 50 ohmios de resistencia de radiación y una resistencia de pérdidas tan solo de 0,5 ohmios: las pérdidas en esta resistencia serían del orden de 1 centésima parte de la potencia radiada. Podemos olvidarnos de ella tranquilamente.
En cambio, si tenemos una antena de tan solo 1 metro de longitud para la banda de 20 metros, su resistencia de radiación estaría alrededor de 1 ohmio y resulta que tiene también una resistencia de pérdidas de 0,5 ohmios, así que nos encontraremos con que vamos a perder un 33% de la energía calentando nuestro radiante de tan solo 1 metro. El negocio empieza a tambalearse y empieza a ser un mal negocio.
Así que ya puedes imaginar lo que sucede con una antena de tan solo 1 metro de longitud en la banda de 80 metros, que tendrá una resistencia de radiación alrededor de 0,1 ohmios con una resistencia de pérdidas de 0,5 ohmios. Podemos llegar a perder hasta el 80% de la energía en forma de calor en nuestra antena o en el acoplador que utilicemos para adaptarla. Muy mal negocio. Según la potencia que apliquemos, nuestra antena será más eficaz transmitiendo señales de humo que no RF útil. Yo lo comprobé un día enviando señales de humo desde la bobina de un acoplador que se ponía al rojo al recibir 200 W de un transmisor de válvulas.
Cable mejor que hilo de cobre
Para compensar en cierta manera el efecto Skin o pelicular, cuando se trata de cables largos, se prefiere utilizar cables formados por varios hilos de cobre, antes que utilizar un hilo de cobre de un solo hilo conductor. De esta forma se consigue una mayor superficie conductora, y se disminuye la resistencia de pérdidas, gracias a la mayor superficie conductora de los hilos múltiples, mucho mayor que la que tendríamos con tan solo la superficie cilíndrica de un conductor de hilo único.
Por este motivo se procura realizar todas las antenas con cable de cobre de hilos múltiples retorcidos, antes que un solo hilo y las tomas de tierra se deben realizar siempre también con malla de cobre, mejor que con cable de de un solo hilo conductor.
La onda electromagnética radiada por la antena.
La combinación del campo eléctrico de signo opuesto creado entre las puntas A y B y el campo magnético creado por la corriente en el centro del dipolo entre C y C’ produce unos campos magnéticos entrelazados que dan vida a una onda electromagnética autónoma que se propaga por el espacio circundante, de modo que puede alejarse y viajar de forma autónoma por el espacio en forma de lo que llamamos onda electromagnética.
La energía de la onda se va intercambiando entre ambos campos, el eléctrico y el magnético, del mismo modo que un circuito resonante paralelo intercambia energía desde el campo magnético de la bobina al campo eléctrico del condensador (Figura 10). Los electrones pasan de la armadura inferior del condensador C en el lado A, al lado superior del condensador C en el lado B. Y viceversa, intercambiando la energía electrostática de C con la energía electromagnética en la inductancia L.
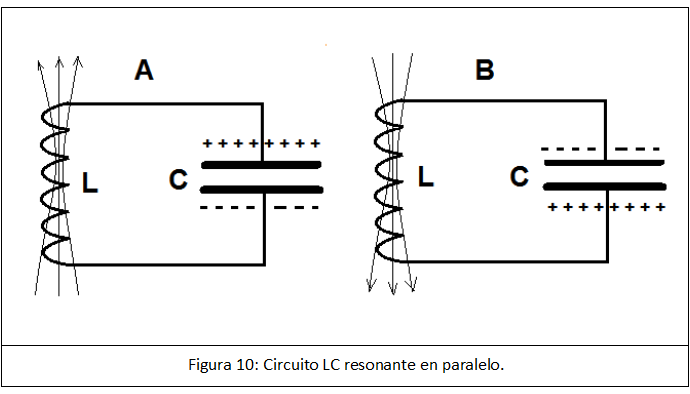
Tenemos un símil de la antena como un circuito resonante en paralelo (o en serie) cuyas armaduras se separan a ambos extremos de la antena como vemos en la parte superior de la figura 11.
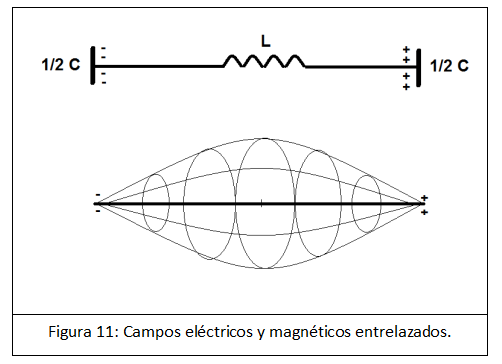
En una antena de media onda resonante, el campo eléctrico entre ambas puntas con tensión opuesta, al colapsarse y cambiar de signo da lugar a una corriente en el centro que crea un campo magnético intenso y este campo magnético da lugar a un nuevo campo eléctrico de polaridad opuesta, que nuevamente da lugar a un nuevo campo magnético opuesto.
Ambos campos quedan entrelazados a 90 grados en el tiempo y en el espacio, de forma que se convierten en una onda electromagnética, cuya energía contenida en el frente de esta onda electromagnética es constante y avanzará de forma autónoma por el aire y el espacio vacío (Figura 11).
Atenuación con el cuadrado de la distancia
Lamentablemente esta energía va disminuyendo en intensidad a medida que en su avance se amplía la esfera en cuyo centro se encontraba la antena emisora, puesto que va aumentando de radio, de modo que se distribuye la misma energía por una superficie de una esfera cada vez mucho mayor, por su mayor radio (la distancia hasta el emisor).
Como la superficie de una esfera aumenta con el cuadrado del radio (S = 4πR2), la densidad de energía de la onda electromagnético (o sea la energía de la onda por metro cuadrado) queda dividida por 4 cada vez que se dobla la distancia, es decir, se dobla el radio R de la esfera cuyo centro es la antena, lo que significa que se atenúa en -6 dB, cada vez que se dobla la distancia cubierta desde el centro emisor, al avanzar por la atmósfera o el espacio vacío (Figura 12).
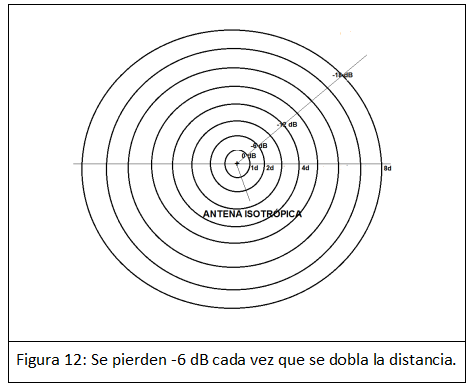
Así por ejemplo, si una señal de 144 MHz nos marca -40 dBm en el Smeter a 1 km, si nos alejamos a 2 km la señal disminuirá en -6 dB (-46 dBm) y si nos alejamos a 4 km la señal disminuirá en -12 dB (marcando por tanto -52 dBm en nuestro medidor). Finalmente si nos alejamos a 8 km, el Smeter nos marcará -58 dBm.
¿Estáis convencidos de que las ondas electromagnéticas de RF existen? ¿Tenéis fe en la radiofrecuencia? Pues no dejéis de utilizarla.
73 Luis EA3OG - ea3og@ure.es


